



suivant: Variance et écart-type
monter: L'espérance mathématique
précédent: Variable centrée
Table des matières
[13] Un système de monitoring est constitué de modules qui peuvent
être montés en série ou en parallèle. Le montage est dit série
si la défaillance d'un seul module entraîne la défaillance de tout le
système ; il est dit parallèle si la défaillance de tous les
modules est nécessaire pour qu'il y ait défaillance de tout le système.
La fiabilité (ou probabilité de survie) d'un module est 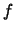 ; sa
probabilité de défaillance est
; sa
probabilité de défaillance est 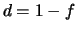 .
Système série
.
Système série
- Quelle est la fiabilité
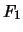 d'un système composé de 10 modules, de
fiabilités
d'un système composé de 10 modules, de
fiabilités 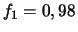 , montés en série ? (Réponse :
, montés en série ? (Réponse :
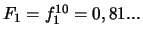 )
)
- Quelle serait la fiabilité
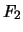 d'un système composé de 9 modules
de fiabilités
d'un système composé de 9 modules
de fiabilités 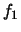 et d'1 module de fiabilité
et d'1 module de fiabilité 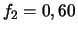 , montés
en série ? (Réponse :
, montés
en série ? (Réponse :
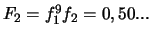 )
)
- Quelle valeur devrait avoir la fiabilité
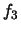 de 10 modules montés en
série pour que la fiabilité du système composé de ces
modules, soit supérieure ou égale à
de 10 modules montés en
série pour que la fiabilité du système composé de ces
modules, soit supérieure ou égale à 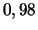 ? (Réponse :
? (Réponse :
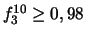 , d'où
, d'où
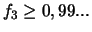 )
)
- 10 modules sont choisis au hasard dans un lot de
fabrication dont on sait que 96 pourcents des modules ont une fiabilité
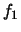 et les autres ont une fiabilité
et les autres ont une fiabilité 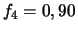 .
.
- Quelle est la probabilité
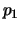 d'obtenir un système série de
fiabilité maximale ? (Réponse :
d'obtenir un système série de
fiabilité maximale ? (Réponse :
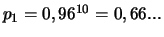 )
)
- Quelle est la probabilité
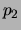 d'obtenir un système série de
fiabilité minimale ? (Réponse :
d'obtenir un système série de
fiabilité minimale ? (Réponse :
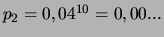 )
)
- Un contrôle de fabrication permettrait de diminuer le pourcentage des
modules de fiabilités
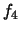 . A quel niveau de contrôle doit-il amener ce
pourcentage
. A quel niveau de contrôle doit-il amener ce
pourcentage 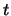 pour que la probabilité
pour que la probabilité 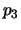 d'obtenir un système
série de fiabilité maximale soit supérieure à
d'obtenir un système
série de fiabilité maximale soit supérieure à 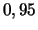 ?
(Réponse :
?
(Réponse :
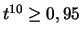 d'où
d'où 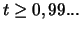 )
)
Système parallèle
- Quelle est la fiabilité
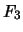 d'un système composé de 10 modules, de
fiabilités
d'un système composé de 10 modules, de
fiabilités 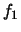 , montés en parallèle ? (Réponse :
, montés en parallèle ? (Réponse :
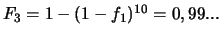 )
)
- Quelle serait la fiabilité
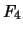 d'un système composé de 9 modules
de fiabilités
d'un système composé de 9 modules
de fiabilités 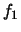 et d'1 module de fiabilité
et d'1 module de fiabilité 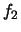 , montés
en parallèle ? (Réponse :
, montés
en parallèle ? (Réponse :
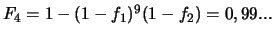 )
)
- Quelle valeur devrait avoir la fiabilité
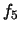 de 10 modules montés en
parallèle pour que la fiabilité du système composé de ces
modules, soit supérieure ou égale à
de 10 modules montés en
parallèle pour que la fiabilité du système composé de ces
modules, soit supérieure ou égale à 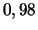 ? (Réponse :
? (Réponse :
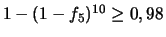 ,
d'où
,
d'où
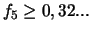 )
)
Protection par redondance
Afin d'assurer le bon fonctionnement du monitoring, on envisage de monter en
parallèle des ensembles (E) de modules montés en série.
- Quelle serait la fiabilité
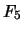 d'un montage en parallèle de deux
ensembles
d'un montage en parallèle de deux
ensembles 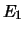 constitués de dix modules de même fiabilité
constitués de dix modules de même fiabilité 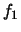 montés en série ? (Réponse :
montés en série ? (Réponse :
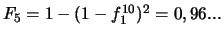 )
)
- Quelle serait la fiabilité
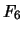 d'un montage en parallèle de deux
ensembles
d'un montage en parallèle de deux
ensembles 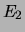 constitués de dix modules de même fiabilité
constitués de dix modules de même fiabilité 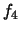 montés en série ? (Réponse :
montés en série ? (Réponse :
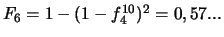 )
)
- Combien d'ensembles
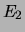 devrait-on monter en parallèle pour que la
fiabilité de ce montage soit au moins égale à
devrait-on monter en parallèle pour que la
fiabilité de ce montage soit au moins égale à 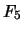 ?
(Réponse :
?
(Réponse :
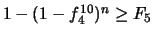 d'où
d'où 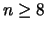 )
)
Evolution temporelle d'une fiabilité : modèle exponentiel
Dans ce modèle, on admet que la probabilité de défaillance d'un module
dans l'intervalle de temps
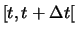 , sachant qu'elle ne survient pas dans l'intervalle de temps
, sachant qu'elle ne survient pas dans l'intervalle de temps ![$[0,t]$](img653.png) , est proportionnelle à la durée
, est proportionnelle à la durée
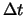 de cet intervalle, c'est-à-dire de la forme
de cet intervalle, c'est-à-dire de la forme 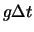 ,
expression dans laquelle
,
expression dans laquelle 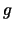 est une constante de proportionalité.
est une constante de proportionalité.
- Soit
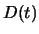 la fonction de répartition temporelle des probabilités
de défaillance. Montrer que
la fonction de répartition temporelle des probabilités
de défaillance. Montrer que
 . (Réponse :
. (Réponse :
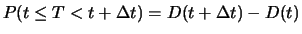 où
où 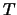 est la variable
aléatoire donnant l'instant où la défaillance survient)
est la variable
aléatoire donnant l'instant où la défaillance survient)
- En faisant tendre
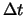 vers
vers 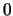 , trouver une équation
différentielle à variables séparables dont on déduira
, trouver une équation
différentielle à variables séparables dont on déduira 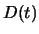 et la
fonction de densité
et la
fonction de densité 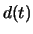 correspondante. (Réponse :
correspondante. (Réponse :
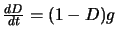 ;
;
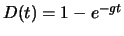 et
et 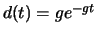 )
)
- Déduire de
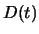 , l'expression de la fonction de répartition
temporelle
, l'expression de la fonction de répartition
temporelle 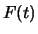 des fiabilités. Calculer la probabilité d'une
fiabilité de 1 an en supposant
des fiabilités. Calculer la probabilité d'une
fiabilité de 1 an en supposant 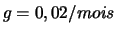 . (Réponse :
. (Réponse : 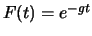 ;
;
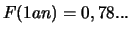 )
)
- Calculer le temps moyen
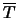 des défaillance et en déduire
le temps moyen des fiabilités. (Réponse :
des défaillance et en déduire
le temps moyen des fiabilités. (Réponse :
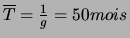 ;
;
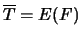 )
)
- Calculer la probabilité d'observer une défaillance entre 1 et 2 ans.
(Réponse :
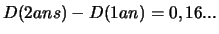 )
)
- Exprimer, en fonction du temps, la fiabilité d'un système
série, puis d'un système parallèle, constitués de 10
modules. Calculer la probabilité de survie à 1 an de chacun de ces
systèmes. (Réponse :
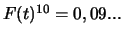 série ;
série ;
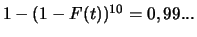 parallèle)
parallèle)




suivant: Variance et écart-type
monter: L'espérance mathématique
précédent: Variable centrée
Table des matières
Vekemans
2002-06-24
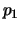 d'obtenir un système série de
fiabilité maximale ? (Réponse :
d'obtenir un système série de
fiabilité maximale ? (Réponse :
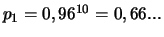 )
)
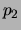 d'obtenir un système série de
fiabilité minimale ? (Réponse :
d'obtenir un système série de
fiabilité minimale ? (Réponse :
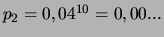 )
)
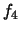 . A quel niveau de contrôle doit-il amener ce
pourcentage
. A quel niveau de contrôle doit-il amener ce
pourcentage 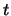 pour que la probabilité
pour que la probabilité 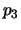 d'obtenir un système
série de fiabilité maximale soit supérieure à
d'obtenir un système
série de fiabilité maximale soit supérieure à 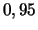 ?
(Réponse :
?
(Réponse :
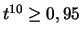 d'où
d'où 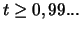 )
)