



suivant: Inégalité de Markov
monter: Variance et écart-type
précédent: Variable réduite
Table des matières
[13] On suppose que la durée de vie d'un individu est une variable
aléatoire continue dont la densité de probabilité 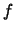 est donnée par
est donnée par
- Déterminez
 pour que
pour que 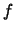 soit effectivement une densité de
probabilité
soit effectivement une densité de
probabilité
Réponse :



![$\Longleftrightarrow \left[
\frac{t^5}{5}-10^2\frac{t^4}{2}+10^4\frac{t^3}{3} \right]_{0}^{100}
=\frac{1}{k}$](img681.png)
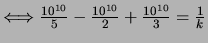

 .
.
- Calculez l'espérance mathématique de la durée de vie
d'un individu, puis l'écart-type.
Réponses :

![$\Longleftrightarrow E(X)=k \left[
\frac{t^6}{6}-2.10^2\frac{t^5}{5}+10^4\frac{t^4}{4} \right]_{0}^{100}$](img686.png)


D'autre part,

![$\Longleftrightarrow E(X^2)=k \left[
\frac{t^7}{7}-2.10^2\frac{t^6}{6}+10^4\frac{t^5}{5} \right]_{0}^{100}$](img690.png)


Il s'ensuit que

- Calculez la probabilité pour qu'un
individu meure entre 30 et 60 ans
Réponse :

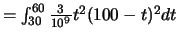
![$=\frac{3}{10^9} \left[
\frac{t^5}{5}-10^2\frac{t^4}{2}+10^4\frac{t^3}{3} \right]_{30}^{60}$](img696.png)
 .
.
Vekemans
2002-06-24


![$\Longleftrightarrow \left[
\frac{t^5}{5}-10^2\frac{t^4}{2}+10^4\frac{t^3}{3} \right]_{0}^{100}
=\frac{1}{k}$](img681.png)
![$\Longleftrightarrow E(X)=k \left[
\frac{t^6}{6}-2.10^2\frac{t^5}{5}+10^4\frac{t^4}{4} \right]_{0}^{100}$](img686.png)
![$\Longleftrightarrow E(X^2)=k \left[
\frac{t^7}{7}-2.10^2\frac{t^6}{6}+10^4\frac{t^5}{5} \right]_{0}^{100}$](img690.png)
![$=\frac{3}{10^9} \left[
\frac{t^5}{5}-10^2\frac{t^4}{2}+10^4\frac{t^3}{3} \right]_{30}^{60}$](img696.png)