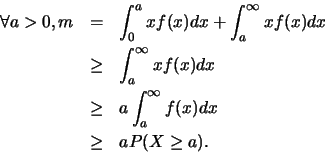suivant: Inégalité de Bienaymé-Tchebychev
monter: Variables aléatoires réelles continues
précédent: Exercice
Table des matières
Soit la variable aléatoire réelle continue  à valeurs non négatives,
d'espérance mathématique
à valeurs non négatives,
d'espérance mathématique  .
Alors,
.
Alors,
Démonstration
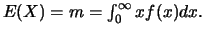
Donc,
Il s'ensuit que
Vekemans
2002-06-24