suivant: Exercice
monter: Probabilité
précédent: Exercice
Table des matières
On tire 4 cartes sans remise dans un jeu de 32 cartes.
On note  ,
, 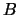 , et
, et  les événements suivants :
les événements suivants :
 Les 4 cartes sont rouges
Les 4 cartes sont rouges
(Réponse :
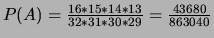 ).
).
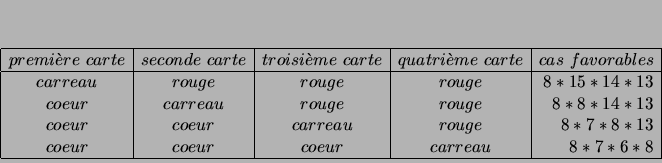
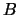 Une seule de ces 4 cartes est un as
Une seule de ces 4 cartes est un as
(Réponse :
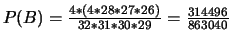 ).
).
 L'une de ces 4 cartes au moins est un carreau
L'une de ces 4 cartes au moins est un carreau
(Réponse :
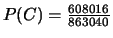 ).
).
Calculer
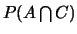 .
Réponse :
.
Réponse :
Donc
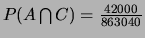 .
Calculer
.
Calculer
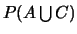 .
Réponse :
.
Réponse :
Donc
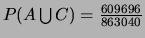 .
.
Vekemans
2002-06-24