



suivant: Le théorème de Bayes
monter: Probabilité conditionnelle, indépendance
précédent: Exercice
Table des matières
On dit que  et
et 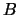 sont indépendants si
sont indépendants si 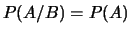 .
On pourra remarquer que
.
On pourra remarquer que
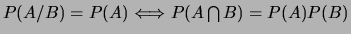 .
Propriété
Soient
.
Propriété
Soient  et
et 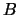 deux événements indépendants.
Alors :
deux événements indépendants.
Alors :
 et
et 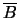 sont indépendants
Démonstration
sont indépendants
Démonstration
 et
et
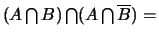 Ø.
Ø.
Donc,
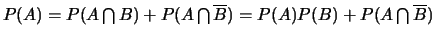 .
.
Donc
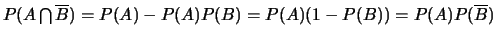 , ce
qui montre que
, ce
qui montre que  et
et 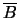 sont indépendants.
sont indépendants.
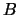 et
et 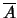 sont indépendants
Démonstration La démonstration est la même que
précédemment en interchangeant les rôles de
sont indépendants
Démonstration La démonstration est la même que
précédemment en interchangeant les rôles de  et
et 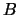 .
.
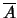 et
et 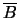 sont indépendants
Démonstration On a montré que
sont indépendants
Démonstration On a montré que  et
et 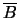 sont indépendants, d'après le premier point, donc,
d'après le second point,
sont indépendants, d'après le premier point, donc,
d'après le second point, 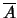 et
et 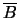 sont
indépendants.
sont
indépendants.
Vekemans
2002-06-24