



suivant: Exercice
monter: Probabilité conditionnelle, indépendance
précédent: Indépendance en probabilité
Table des matières
Soit un référentiel  , et soient
, et soient
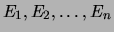 formant une partition de
formant une partition de  .
.
 tel que
tel que  ,
, 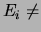 Ø.
Ø.
 tel que
tel que 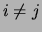 ,
,
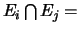 Ø
(incompatibles)
Ø
(incompatibles)
-
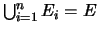
Alors,
 (formule dite des probabilités totales),
et
(formule dite des probabilités totales),
et
 Démonstration
Démonstration
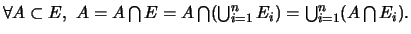
Si  ,
,  et
et  sont
incompatibles car
sont
incompatibles car  et
et  le sont.
le sont.
Donc,
 .
.
De plus

Vekemans
2002-06-24
 Démonstration
Démonstration
