Exercice

[13] Soit une voiture M de marque X. Cette voiture démarre mal. Cependant, le garagiste sait que parmi les véhicules qui démarrent mal, la probabilité pour que la cause en soit le démarreur est 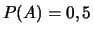$P(A)=0,5$, que la cause en soit la batterie est 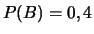$P(B)=0,4$, puis que la cause en soit les bougies est $P(C)=0,1$. De plus, sur le nombre total de voitures démarrant mal à cause du démarreur, 10 pourcents sont de marque X, sur le nombre total de voitures démarrant mal à cause de la batterie, 20 pourcents sont de marque X, et sur le nombre total de voitures démarrant mal à cause des bougies, 5 pourcents sont de marque X. Sachant cela aussi, le garagiste se penchera-t-il d'abord sur le démarreur, la batterie ou les bougies ? Solution : $X$ est l'événement être de marque X.
$P(X/A)=0,1 ; P(X/B)=0,2 ; P(X/C)=0,05$.
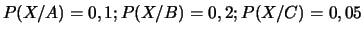Calculons 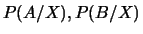$P(A/X), P(B/X)$ et $P(C/X)$.

$$P(A/X)=\frac{0,5*0,1}{0,5*0,1+0,4*0,2+0,1*0,05}=0,37...$$

$$P(B/X)=\frac{0,4*0,2}{0,5*0,1+0,4*0,2+0,1*0,05}=0,59...$$

$$P(C/X)=\frac{0,1*0,05}{0,5*0,1+0,4*0,2+0,1*0,05}=0,04...$$

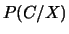Le garagiste vérifiera donc d'abord la batterie.