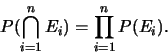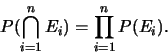suivant: Indépendance deux à deux
monter: Probabilité conditionnelle, indépendance
précédent: Exercice
Table des matières
Soient
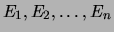 ,
,  événements. On dit que
tous ceux-ci sont mutuellement indépendants si
événements. On dit que
tous ceux-ci sont mutuellement indépendants si
Exemple On lance un dé équilibré à huit
faces.
On note 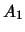 l'événement obtenir 1,2,7 ou 8,
l'événement obtenir 1,2,7 ou 8,
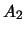 l'événement obtenir 2,3,6 ou 8 et
l'événement obtenir 2,3,6 ou 8 et
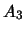 l'événement obtenir 3,4,5 ou 8.
l'événement obtenir 3,4,5 ou 8.
Ainsi, 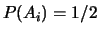 ,
,
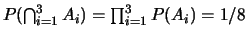 .
.
On a :
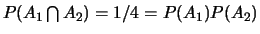 ,
,
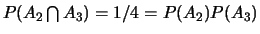 ,
,
mais,
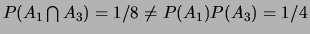 .
.
Vekemans
2002-06-24