



suivant: Indépendance totale d'un nombre
monter: Probabilité conditionnelle, indépendance
précédent: Indépendance mutuelle d'un nombre
Table des matières
Soient
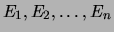 ,
,  événements. On dit qu'ils
sont indépendants deux à deux si
événements. On dit qu'ils
sont indépendants deux à deux si  tel que
tel que 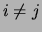 , on ait
, on ait
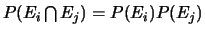 .
Exemple On lance successivement 2 dés à 6 faces.
.
Exemple On lance successivement 2 dés à 6 faces.
On note 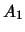 l'événement obtenir un nombre pair avec la
premier dé,
l'événement obtenir un nombre pair avec la
premier dé, 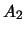 l'événement obtenir un nombre impair
avec le second dé et
l'événement obtenir un nombre impair
avec le second dé et 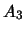 l'événement obtenir deux
dés de même parité.
l'événement obtenir deux
dés de même parité.
Ainsi, 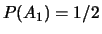 ,
, 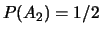 et
et 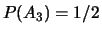 .
.
On a :
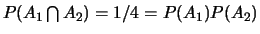 ,
,
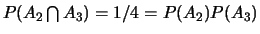 ,
,
et
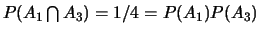 .
.
Mais,
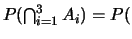 Ø
Ø
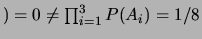 .
Conclusion
.
Conclusion
Il n'y a aucune implication entre indépendance deux
à deux et indépendance mutuelle.
Vekemans
2002-06-24