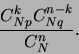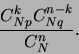suivant: Exercice
monter: Epreuves répétées
précédent: Epreuves répétées non exhaustives
Table des matières
Soit  un référentiel partitionné en deux événements
notés
un référentiel partitionné en deux événements
notés  et
et 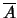 . L'événement
. L'événement  est celui de
tirer une boule blanche dans une urne parmi des blanches et des
noires. Les probabilités de ces deux événements sont
données par
est celui de
tirer une boule blanche dans une urne parmi des blanches et des
noires. Les probabilités de ces deux événements sont
données par 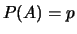 et
et
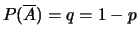 .
L'urne contient au début
.
L'urne contient au début  boules dont
boules dont 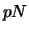 blanches et
blanches et 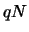 noires. On répète l'épreuve un certain nombre de fois en
modifiant le référentiel. Pendant les
noires. On répète l'épreuve un certain nombre de fois en
modifiant le référentiel. Pendant les  épreuves,
épreuves, 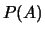 va varier. C'est le cas d'un tirage sans remise, ...
La probabilité que
va varier. C'est le cas d'un tirage sans remise, ...
La probabilité que  soit réalsé exactement
soit réalsé exactement  fois, à
l'issue de
fois, à
l'issue de  épreuves, sans tenir compte de l'ordre est
épreuves, sans tenir compte de l'ordre est
Nous aurons l'occasion de retrouver ce résultat lorsque
nous étudierons la loi hypergéométrique.
Vekemans
2002-06-24