



suivant: Exercice
monter: Epreuves répétées
précédent: Epreuves répétées exhaustives
Table des matières
On considère 30 sujets de CAPES. 20 exactement contiennent de
l'analyse numérique (AN) et 4 exactement, des probabilités
(P). L'un des sujets contient à la fois de l'analyse numérique
et des probabilités.
Dans ce lot de sujets,
- on prend au hasard l'un d'eux. Quelle est la probabilité
pour qu'il contienne soit de l'analyse numérique, soit des
probabilités.
(Réponse :
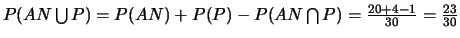 ).
).
- on prend au hasard 3 d'entre eux avec remise (A). Quelle est
la probabilité pour qu'ils contiennent tous soit de l'analyse
numérique, soit des probabilités.
(Réponse :
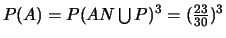 ).
).
- on prend au hasard 3 d'entre eux sans remise (B). Quelle est
la probabilité pour qu'ils contiennent tous soit de l'analyse
numérique, soit des probabilités.
(Réponse :
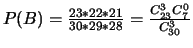 ).
).
Vekemans
2002-06-24