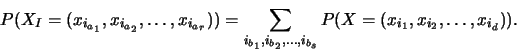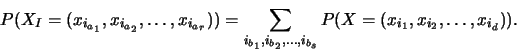suivant: Loi conditionnelle, indépendance de
monter: Lois de probabilités
précédent: Exemple
Table des matières
Soit un vecteur de variables aléatoires réelles
discrètes  ,
,
 ,
prenant ses valeurs dans
,
prenant ses valeurs dans
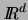 .
Par définition, la probabilité que
.
Par définition, la probabilité que
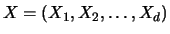 soit égale à
soit égale à
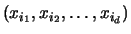 est la probabilité des éléments de
est la probabilité des éléments de
 ayant pour image
ayant pour image
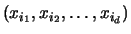 par
par  .
Elle est notée :
.
Elle est notée :
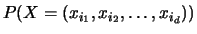 .
La loi de probabilité d'une variable aléatoire réelle discrète
.
La loi de probabilité d'une variable aléatoire réelle discrète  est
définie par les valeurs de ces probabilités
est
définie par les valeurs de ces probabilités
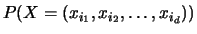 qui doivent vérifier
qui doivent vérifier
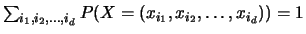 .
Si on suppose donnée la loi de
.
Si on suppose donnée la loi de  , on appelle loi marginale de
, on appelle loi marginale de 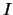 la loi de
la loi de
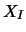
(où
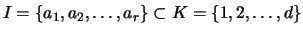 ,
,
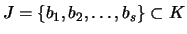 tels que
tels que 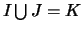 ,
, 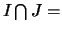 Ø, avec
Ø, avec 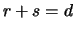 )
)
dont la probabilité
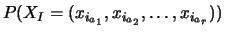 est donnée par la formule
est donnée par la formule
Vekemans
2002-06-24