



suivant: Fonction de répartition ou
monter: Lois de probabilités
précédent: Loi d'un vecteur de
Table des matières
Soient  et
et  deux variables aléatoires réelles discrètes, on peut donner la
définition de la loi conditionnelle de la variable aléatoire réelle discrète
deux variables aléatoires réelles discrètes, on peut donner la
définition de la loi conditionnelle de la variable aléatoire réelle discrète
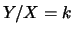 (on lit
(on lit  sachant que
sachant que 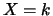 ) par la probabilité :
) par la probabilité :
Soient  et
et  deux variables aléatoires réelles discrètes, on dit que
deux variables aléatoires réelles discrètes, on dit que  et
et  sont deux variables aléatoires réelles discrètes indépendantes si
sont deux variables aléatoires réelles discrètes indépendantes si
On peut définir l'indépendance deux à deux, mutuelle ou totale de  variables aléatoires réelles discrètes en calquant celles sur
variables aléatoires réelles discrètes en calquant celles sur  événements.
événements.
Vekemans
2002-06-24