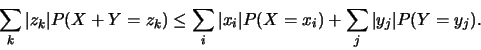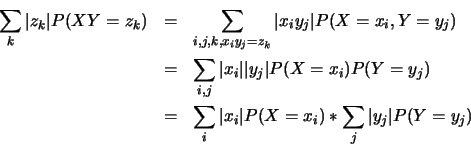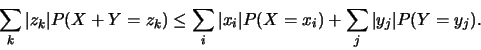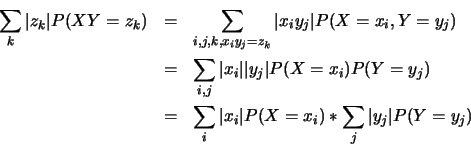suivant: Variable centrée
monter: L'espérance mathématique
précédent: Exemple -suite du 4.2.1.-
Table des matières
- Pour toute constante
 ,
, 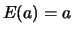 (trivial)
(trivial)
- Pour toute constante
 ,
, 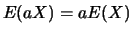 (trivial)
(trivial)
-
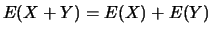 (démonstration hors programme)
Démonstration
Montrons d'abord que si
(démonstration hors programme)
Démonstration
Montrons d'abord que si  et si
et si 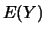 existent, alors,
existent, alors, 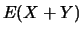 aussi.
aussi.
On a
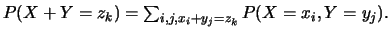
Cependant,
car
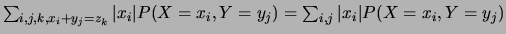
et car
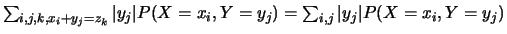 .
.
Or
 et
et
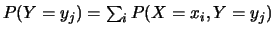 ,
d'après la définition d'une loi marginale.
Donc
,
d'après la définition d'une loi marginale.
Donc
Il s'ensuit que la série 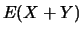 est absolument convergente et donc
convergente.
est absolument convergente et donc
convergente.
Pour montrer que
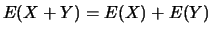 , il suffit maintenant de réécrire les
lignes précédentes en enlevant les valeurs absolues et en remplaçant
les inégalités par des égalités.
, il suffit maintenant de réécrire les
lignes précédentes en enlevant les valeurs absolues et en remplaçant
les inégalités par des égalités.
-
 (trivial)
(trivial)
- Lorsque
 et
et  sont indépendantes, on a
sont indépendantes, on a
 Démonstration
Montrons d'abord que si
Démonstration
Montrons d'abord que si  et si
et si 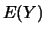 existent, alors,
existent, alors, 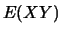 aussi.
aussi.
On a :
On a pu écrire
 car les variables
sont indépendantes.
car les variables
sont indépendantes.
On a montré que la série 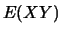 est absolument convergente et donc
convergente.
est absolument convergente et donc
convergente.
Pour montrer que
 , il suffit maintenant de réécrire les
lignes précédentes en enlevant les valeurs absolues.
, il suffit maintenant de réécrire les
lignes précédentes en enlevant les valeurs absolues.




suivant: Variable centrée
monter: L'espérance mathématique
précédent: Exemple -suite du 4.2.1.-
Table des matières
Vekemans
2002-06-24