



suivant: Covariance, régression et corrélation
monter: Variance et écart-type
précédent: Variable réduite
Table des matières
Soient  et
et  deux variables aléatoires réelles discrètes. On définit alors
la variance conditionnelle de
deux variables aléatoires réelles discrètes. On définit alors
la variance conditionnelle de 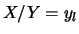 par :
par :
ou par :
d'après la troisième propriété relative à la variance.
Il s'ensuit que nous obtenons le résultat suivant :
Démonstration
On a :
Donc,
Vekemans
2002-06-24
![\begin{eqnarray*}
% latex2html id marker 814
& &\sum_l V(X/Y=y_l) P(Y=y_l) ...
... marginale)}\\
&=& E(X^2) - \sum_l [E(X/Y=y_l)]^2 P(Y=y_l)
\end{eqnarray*}](img341.png)
![\begin{eqnarray*}
V(X)&=&E(X^2)-[E(X)]^2 \\
&=& \sum_l \left(V(X/Y=y_l)+[E(X/Y=y_l)]^2\right) P(Y=y_l) -[E(X)]^2
\end{eqnarray*}](img342.png)