



suivant: Variance conditionnelle
monter: Variance et écart-type
précédent: Propriétés de la variance
Table des matières
On dit qu'une variable aléatoire réelle discrète  est réduite si elle est de variance
est réduite si elle est de variance
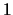 .
Si on considère une variable aléatoire réelle discrète
.
Si on considère une variable aléatoire réelle discrète  de variance
de variance
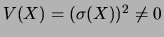 (non nécessairement égale à 1), alors la
variable aléatoire réelle discrète
(non nécessairement égale à 1), alors la
variable aléatoire réelle discrète 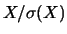 est réduite.
En effet,
est réduite.
En effet,
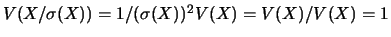 .
Si on considère une variable aléatoire réelle discrète
.
Si on considère une variable aléatoire réelle discrète  d'espérance mathématique
d'espérance mathématique
 et de variance
et de variance
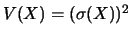 ,
alors la variable aléatoire réelle discrète
,
alors la variable aléatoire réelle discrète
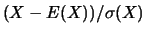 est centrée et réduite.
est centrée et réduite.
Vekemans
2002-06-24