



suivant: Exemple -suite du 4.2.1.-
monter: Variables aléatoires réelles discrètes
précédent: Espérance conditionnelle
Table des matières
Lorsque les quantités
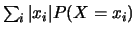 et
et
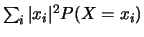 sont définies, on appelle variance d'une variable aléatoire réelle discrète
sont définies, on appelle variance d'une variable aléatoire réelle discrète
 , et on note
, et on note 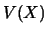 la quantité :
la quantité :
L'écart-type est alors défini par
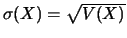 .
.
Sous-sections
Vekemans
2002-06-24