La géométrie
    Denis Vekemans
    Maître de conférences au Centre IUFM de Gravelines
    Utilisez ce lien pour me faire part de vos remarques et suggestions.
    La géométrie dans l'espace
    Droites et plans dans l'espace
    Droites dans l'espace
    Théorème
    Par deux points non confondus passe une unique droite.
    Théorème
    Deux droites sont parallèles dans l'espace si elles sont coplanaires dans P et sont parallèles dans P.
    Théorème
    Deux droites sont orthogonales dans l'espace si leurs parallèles menées par un point donné sont perpendiculaires dans le plan défini par ces deux droites.
    L'énoncé de ce théorème utilise un théorème quelque peu plus bas.
    Plans dans l'espace
    Théorème
    Par trois points non alignés et non confondus passe un unique plan.
    Théorème
    Par deux droites sécantes non confondues passe un unique plan.
    Théorème
    Deux plans P et P' sont parallèles dans l'espace si toute droite de P est parallèle à au moins une droite de P'.
    Note : il suffit de le vérifier pour deux droites non parallèles de P.
    Théorème
    Deux plans P et P' sont orthogonaux dans l'espace si P' contient au moins une droite D qui soit orthogonale à P.
    L'énoncé de ce théorème utilise un théorème quelque peu plus bas.
    Théorème
    Une droite D est parallèle à un plan P dans l'espace si au moins un plan P' contenant D est parallèle à P.
    Théorème
    Une droite D est orthogonale à un plan P dans l'espace si toute droite de P est orthogonale à D.
    Note : il suffit de le vérifier pour deux droites non parallèles de P.
    Exercice corrigé

    Vrai ou faux ? Contre-exemple si faux. On considère le cube ABCDEFGH.

    .

    Deux droites parallèles à une même troisième sont parallèles entre-elles.

    Deux droites orthogonales à une même troisième sont parallèles entre-elles.

    Deux plans parallèles à un même troisième sont parallèles entre eux.

    Deux plans orthogonaux à un même troisième sont parallèles entre eux.

    Deux plans parallèles à une même droite sont parallèles entre eux.

    Deux plans orthogonaux à une même droite sont parallèles entre eux.

    Deux plans P et P' sont orthogonaux si toute droite de P est orthogonale à au moins une droite de P'.

    Si P et P' sont deux plans parallèles, si P'' est un plan qui coupe P sur la droite D et qui coupe P' sur la droite D' alors D et D' sont parallèles.

    Si P et P' sont deux plans orthogonaux, si P'' est un plan qui coupe P sur la droite D et qui coupe P' sur la droite D' alors D et D' sont perpendiculaires.

    Les polyèdres
    Définition : Un polyèdre est une figure géométrique délimitée par des polygones.
    Quelques polyèdres usuels : le cube, le parallélipipède recangle (ou le pavé droit), la famille des pyramides (plus particulièrement des pyramides régulères), la famille des prismes (plus particulièrement des prismes droits), ...
    Ils admettent généralement un patron.
    On les représente aussi, plus usuellement, en perspective cavalière.
    D'autres figures dans l'espace
    Le cylindre ... Il admet un patron. Le cercle de base sera vu comme une ellipse sur la perspective cavalière.
    Le cône ... Il admet un patron. Le cercle de base sera vu comme une ellipse sur la perspective cavalière.
    La sphère ... Elle n'admet pas de patron. Elle sera vue comme une ellipse (en général, proche du cercle) en perspective cavalière.
    Différents modes de représentation dans l'espace
    Sur quel solide allons-nous travailler ?
    Soit ABCDEFGH un cube de côté mesurant quatre centimètres. Les faces de ce solide sont des carrés : ABCD, EFGH, ABFE, BCGF, CDHG et DAEH.

.

.

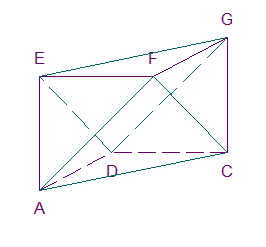
    Nous considérons alors le solide ACDEFG. Les faces de ce solide sont des triangles : ACD, EFG, ACF, DEG, AEF, CFG, CDG et ADE.

.

.

    Remarque : nous avons maintenant moins de sommets et plus de faces.
    Travail sur ces solides
    L'objectif de ce travail est de calculer la hauteur du deuxième solide lorsque ce dernier est posé sur le plan (ACF).
    Nous allons d'abord montrer que les plans (ACF) et (DEG) sont parallèles.
    Montrons que le plan (ACF) est orthogonal à la droite (BH). Pour ce faire, nous allons montrer :
    (BH) ┴ (AC). En effet, le plan (BDF) est orthogonal à la droite (AC) car tout d'abord (BD) ┴ (AC) (les diagonales du carré sont perpendiculaires) et ensuite car (BF) ┴ (AC) (le plan (ABC) étant orthogonal à la droite (BF)). Puis, comme (BDF) ┴ (AC), on déduit (BH) ┴ (AC).
    (BH) ┴ (AF). Nous faisons de même que précédemment ...
    (BH) ┴ (AC) et (BH) ┴ (AF) induisent directement que (BH) ┴ (ACF).
    Par suite, nous montrons de la même façon que (BH) ┴ (DEG).
    Nous avons deux plans qui sont orthogonaux à une même droite (BH), ils sont donc parallèles et (ACF) // (DEG).
    Nous appelons I le point d'intersection de la droite (BH) et du plan (ACF) et J le point d'intersection de la droite (BH) et du plan (DEG). La hauteur du second solide est donc la mesure du segment [IJ].
    Pour calculer cette longueur, nous allons procéder comme suit :
    Calcul de BH ;
    Pythagore appliqué deux fois consécutivement dans le rectangle ABD rectangle en A, puis dans le triangle BDH recatngle en D donne BH = 4 x √3 cm.
    Calcul de JH (pour ce faire, on calcule le volume du tétraèdre DEGH de deux manières différentes, après avoir calculé l'aire du triangle DEG) ;
    Le triangle DEG est équilatéral de côté BH = 4 x √2 cm et Aire(DEG) = (4 x √2) x (4 x √2 x √3/2)/2 cm2 = 8 x √3 cm2. Ensuite, Volume(DEGH) = (HE x HD x HG)/6 = 32/3 cm3, ou Volume(DEGH) = (JH x Aire(DEG))/3 = JH x 8 x √3/3 cm2. Et, enfin, JH = 4 x √3/3 cm.
    Nous déduisons BI (par symétrie) ;
    BI = 4 x √3/3 cm.
    Nous concluons.
    IJ = BH - BI - JH = 4 x √3 - 4 x √3/3 - 4 x √3 cm = 4 x √3/3 cm.
    Définition : Le plan médiateur d'un segment [AB] est l'ensemble des points équidistants de A et de B.
    Théorème : propriétés du plan médiateur d'un segment
    Le plan médiateur du segment [AB] passe par le milieu du segment [AB] et est orthogonal à la droite (AB).
    Si un plan passe par le milieu du segment [AB] et est orthogonal à la droite (AB), alors c'est le plan médiateur du segment [AB].
    Si trois points P, Q et R sont équidistants de A et de B, alors le plan (PQR) est le plan médiateur du segment [AB].
    Et si nous continuions l'analyse des solides :
    Qu'est I pour le triangle ACF ?
    Comme ACF est un triangle équilatéral, il est fort possible que ce point I soit à la fois orthocentre, centre de gravité, centre du cercle circonscrit et centre du cercle inscrit. Il semble plus facile de montrer qu'il est équidistant de chacun des points A, C, et F (et donc centre du cercle circonscrit au triangle ACF).
    Montrons que AI = IC (AB = BC, AF = FC et AD = DC ; d'où (BFD) est le plan médiateur du segment [AC] ; nous concluons car I appartient à ce plan médiateur) ;
    Nous montrons de même que AI = IF.
    IA = IC = IF, donc I est centre du cercle circonscrit au triangle ACF.
    Représentation des faces
    Empreintes
    Représenter chacune des faces du solide ABCDEFGH.
    Représenter chacune des faces du solide ACDEFG.
    Patrons
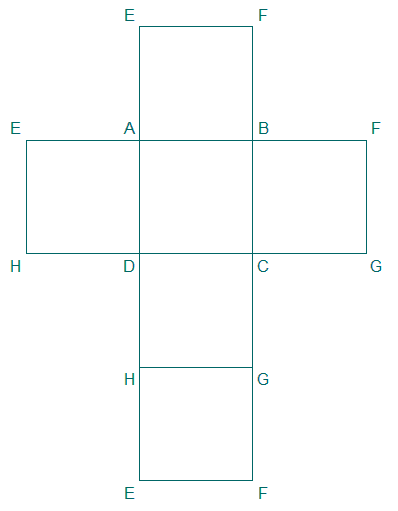
    Représenter un patron du solide ABCDEFGH.
    Remarque : il est écrit un patron.

.

.

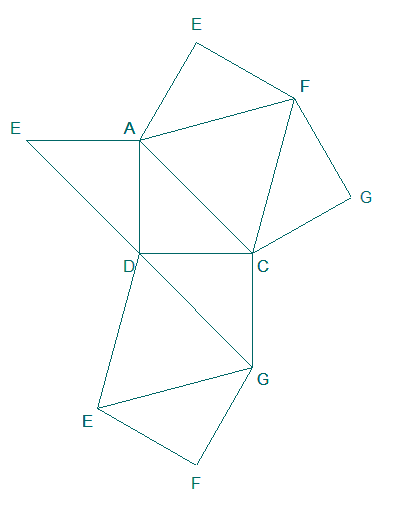
    Représenter un patron du solide ACDEFG.

.

.

    Remarque : lorsque tous les polygones sont réguliers, il est possible de schématiser un patron comme pour le cube :
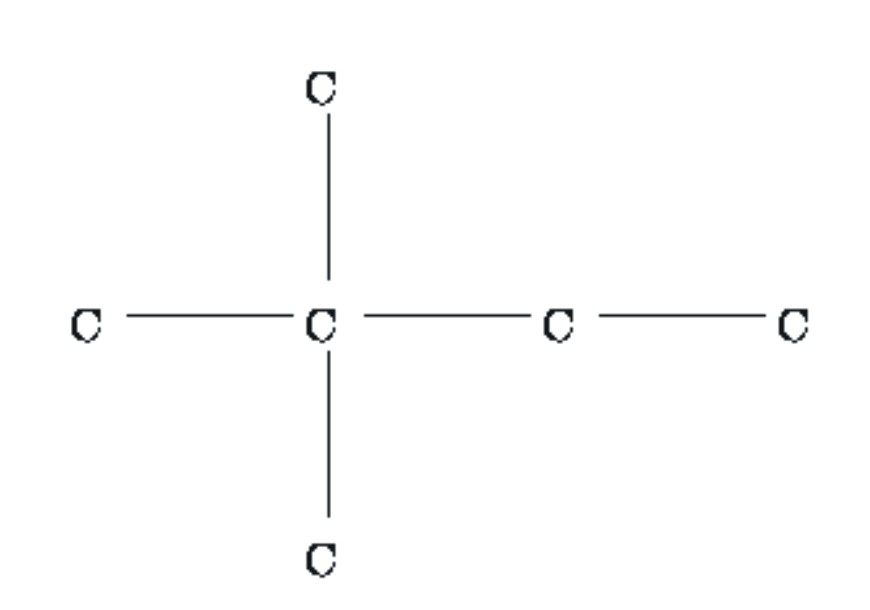
    où C désigne un carré et les liaisons désignent des arêtes qui coïncident.
    Représentation du solide en perspective cavalière
    La face ABFE est vue de face et est par conséquent non déformée ((AB) ou (FE) sont portées par la ligne d'horizon et (AE) ou (BF) sont verticales car ABFE est un carré).
    (AD) ┴ (ABE), (BC) ┴ (ABE), (FG) ┴ (ABE) et (EH) ┴ (ABE).
    Pour cette raison, elle sont appelées fuyantes, et sont, en perspective cavalière, représentées comme faisant un angle d'incidence α avec l'horizon ((AD) // (BC) // (FG) // (EH)).
    Généralement, cet angle α est choisi comme valant 30°, 45° ou 60° (nous allons choisir 45°).
    De plus, sur ces fuyantes, les mesures sont généralement multipliées par un coefficient d'agrandissement/réduction, généralement, 0,5, 0,7, ou 1 (nous choisissons ici ce coefficient égal à 0,7 (cas de réduction)).
    Représenter le solide ABCDEFGH en perspective cavalière.
    Représenter le solide ACDEFG en perspective cavalière.
    Représentation d'un solide en dessin industriel
    Nous allons nous efforcer de compléter le dessin industriel suivant, dont la vue de face est fournie.

.

.

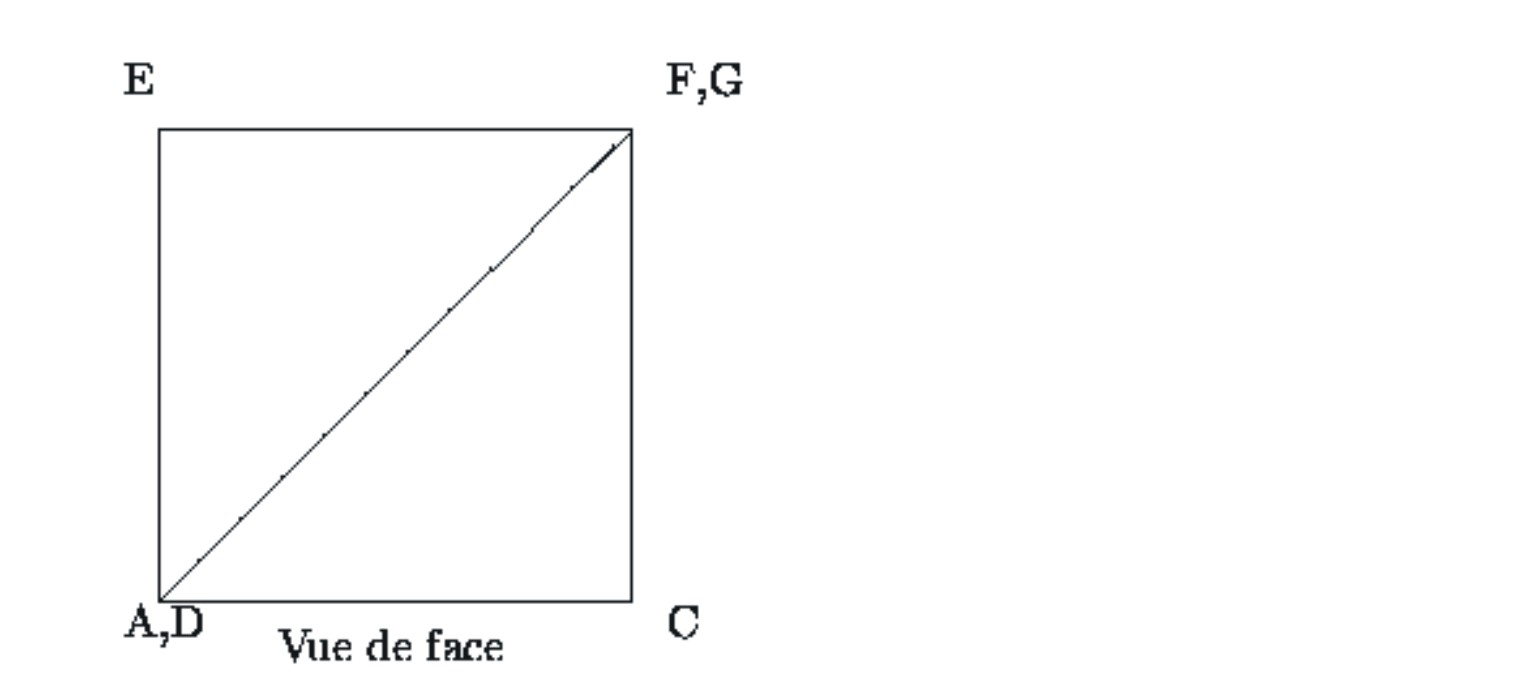
    Représentation d'une coupe d'un solide
    Nous appelons Λ le plan médiateur commun à chacun des segments [AE], [BF], [CG] et [DH].
    Représenter la coupe du solide ABCDEFGH dans le plan Λ.
    Voir le carré PQRS ci-bas.

.

.

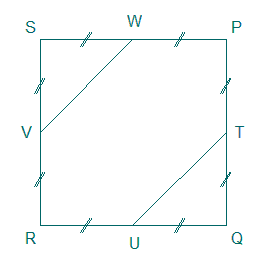
    Représenter la coupe du solide ACDEFG dans le plan Λ.
    Voir l'hexagone PTURVW ci-haut.
    Nous nommons alors Γ ce polygone.

    Analyse sommaire du polygone Γ.

.

    Γ est-il un polygone régulier ?

    Combien Γ possède-t-il d'axes de symétries ?

    Quelles sont les mesures de ses côtés ?

    Quelle est son aire ?

    Il faut savoir que la coupe d'une figure ne représente jamais une figure de l'espace : il ne s'agit que d'une coupe de cette figure.
    Remarque : même une infinité de coupes ne suffit pas à définir un solide de façon non équivoque (par exemple, les tétraèdres ABDE et ABDG ont tous deux les mêmes coupes parallèlement au plan (ABD), mais sont bien entendu différents).
    Liens entre les différents modes de représentation mentionnés
    Les passages entre un mode de représentation et un autre sont bien souvent délicats.
    Ces modes de représentation sont toujours valables pour les polyèdres.
    Mais on peut bien souvent élargir à d'autres figures ce type de représentation :
      Un cône ou un cylindre sont représentables par un patron ..., mais pas une sphère.
      Un cône, un cylindre ou une sphère sont représentables en perpective cavalière. Cependant, pour des surfaces ne présentant pas (ou peu) d'arêtes (comme la sphère), seul le contour doit être représenté et cela peut porter à confusion (c'est pourquoi, dans ce cas, on adjoint généralement une coupe à cette perspective cavalière pour essayer de lever les ambiguïtés (dans le cas de la sphère, on représente souvent l'équateur qui sera vu comme une ellipse, mais qui représente un cercle)).
    Exercice : coupes du cube
Sujet (disciplinaire)
Solution
    Exercice [Martinique, 2000]
Sujet (disciplinaire)
Solution
    Exercice [Limoges, 1998]
Sujet (disciplinaire)
Solution
    Exercice [Bordeaux, Caen, Clermont, Nantes, Orléans-Tours, Poitiers, La Réunion, 2000]
Sujet (disciplinaire)
Solution
    Exercice [Lyon, 1998]
Sujet (disciplinaire)
Solution
    Exercice [Bordeaux, Clermont, Nantes, Poitiers, Ile de la Réunion (2), 1999]
Sujet (disciplinaire)
Solution
    Exercice [Besançon, 1998]
Sujet (disciplinaire)
Solution
    Exercice [Corse, 1998]
Sujet (disciplinaire)
Solution
    Exercice [Toulouse, 1999]
Sujet (disciplinaire)
Solution