Denis Vekemans
Maître de conférences au Centre IUFM
de Gravelines
La
géométrie
La géométrie
plane
Polygones
Généralités
En deux définitions. - Un polygone convexe est une intersection finie de
demi-plans (une figure géométrique du plan
délimitée par des segments est un polygone). On
définit ici un polygone convexe par son intérieur (il
existe des définitions basées sur la frontière
-i.e. le bord-).
- On se limite dans la suite au cas des polygones bornés (i.e. qui peuvent être contenus
dans un disque).
- Un polygone est une réunion
finie de polygones convexes.
- On se limite dans la suite au cas des polygones connexes (i.e. d'un seul tenant).
Un polygone possède un nombre fini de sommets et d'arêtes.
Les polygones peuvent être convexes, concaves ou encore,
croisés.
On dit qu'il sont convexes si chacun des
segments joignant deux sommets est intérieur au polygone.
On dit qu'ils sont concaves dans le cas
contraire.
Un cas particulier des polygones concaves est celui des polygones croisés où au moins deux
côtés non consécutifs, considérés
comme segments, se coupent.
- Théorème
La somme des angles d'un polygone non croisé à n (n
> 2) côtés vaut (n-2) x 180
degrés.
Polygones réguliers
Définition : un polygone
est dit régulier s'il est convexe,
inscriptible dans un cercle et si tous ses côtés,
considérés comme segments, ont même longueur.
Voici pour exemple les polygones réguliers à 3, 4,
5, 6 et 7 côtés.

- Théorème
Un polygone régulier a tous ses angles égaux en mesure.
Triangles
Un triangle est un polygone à trois côtés.
- Exercice corrigé
1. Représenter de façon
ensembliste les triangles scalènes, isocèles et
équilatéraux. Ces patates classifient les
triangles par les longueurs des côtés.
2. Représenter de façon
ensembliste les triangles acutangles, obtusangles, rectangles,
isocèles et équilatéraux. Ces patates
classifient les triangles par les angles.
Droites particulières d'un triangle (dans un triangle ABC)
...
- 1. La hauteur issue de A est
la droite passant par A qui est perpendiculaire à la
droite (BC).
- Le pied de la hauteur issue de A est le point de concours
de la hauteur issue de A et de la droite (BC).
- Par extension, le mot hauteur désigne aussi la distance
entre A et le pied relatif à sa hauteur.
Dans l'animation ci-dessous, en déplaçant le point A,
on peut voir comment se déplace la hauteur du triangle ABC issue de A.
- 2. La médiane issue de A
est le segment dont les extrémités sont A et le
milieu du segment [BC].
- La médiane est également, par abus
de langage, la droite passant par A et par le milieu du segment
[BC].
- Par extension, le mot médiane désigne aussi la
distance entre A et le milieu du segment [BC].
Dans l'animation ci-dessous, en déplaçant le point A,
on peut voir comment se déplace la médiane du triangle ABC issue de A.
- 3. La médiatrice du segment [BC]
est déjà définie. C'est l'une des trois
médiatrices du triangle ABC.
Dans l'animation ci-dessous, en déplaçant le point A,
on peut voir que la médiatrice du triangle ABC relative au segment [BC]
ne dépend pas de A.
- 4. La bissectrice de l'angle
est déjà définie. C'est
la bissectrice issue de A.
- Le pied de la bissectrice issue de A est le point de
concours de la bissectrice issue de A et de la droite (BC).
- Par extension, le mot bissectrice désigne aussi la
distance entre A et le pied relatif à sa bissectrice.
Dans l'animation ci-dessous, en déplaçant le point A,
on peut voir comment se déplace la bissectrice du triangle ABC issue de A.
- Théorème
: points de concours d'un triangle
Les hauteurs, médianes, médiatrices et bissectrices d'un
triangle sont concourrantes. On appelle respectivement les points de
concours l'orthocentre, le centre de gravité, le centre du cercle circonscrit et le centre du cercle inscrit du triangle.
Dans les animations ci-dessous, les points A, B et C sont mobiles
(leur position influe sur celle des points particuliers :
l'orthocentre, le centre de gravité, le centre du cercle circonscrit et le centre du cercle inscrit du triangle).
- Théorème
: centre du cercle circonscrit
Le centre du cercle circonscrit est, comme son nom l'indique, le centre
du cercle circonscrit au triangle. Il est équidistant des trois
sommets de ce triangle.
- Théorème
: centre de gravité
Le centre de gravité du triangle coupe une médiane en
deux parties disjointes (au centre de gravité près) dont
celle contenant le sommet a une longueur double de l'autre.
- Théorème
: utilisation de différents points de concours du triangle
- 1. De l'orthocentre ...
1. Si une droite passe par un sommet d'un triangle et passe par le
point d'intersection de deux des hauteurs de ce triangle, alors c'est
une hauteur de ce triangle.
2. Si une droite est perpendiculaire à un des côtés
d'un triangle et passe par le point d'intersection de deux des hauteurs
de ce triangle, alors c'est une hauteur de ce triangle.
- 2. Du centre de gravité...
1. Si une droite passe par un sommet d'un triangle et passe par le
point d'intersection de deux des médianes de ce triangle, alors
c'est une médiane de ce triangle.
2. Si une droite passe par le milieu d'un des côtés d'un
triangle et passe par le point d'intersection de deux des
médianes de ce triangle, alors c'est une médiane de ce
triangle.
- 3. Du centre du cercle circonscrit
...
1. Si une droite est perpendiculaire à un des côtés
d'un triangle et passe par le point d'intersection de deux des
médiatrices de ce triangle, alors c'est une médiatrice de
ce triangle.
2. Si une droite passe par le milieu d'un des côtés d'un
triangle et passe par le point d'intersection de deux des
médiatrices de ce triangle, alors c'est une médiatrice de
ce triangle.
- 4. Du centre du cercle inscrit ...
Si une droite passe par un sommet d'un triangle et passe par le point
d'intersection de deux des bissectrices de ce triangle, alors c'est une
bissectrice de ce triangle.
- Théorème
: propriétés du triangle rectangle
1. Si un triangle ABC est rectangle en A, alors
la médiane issue de A mesure la moitié de
l'hypoténuse [BC].
Réciproquement, si dans un triangle ABC, la
médiane issue de A mesure la moitié du segment [BC],
alors ce triangle est rectangle en A et le côté [BC]
en est l'hypoténuse.
2. Si un triangle ABC est rectangle en A, alors
l'hypoténuse [BC] est diamètre du cercle
circonscrit. Réciproquement, si un triangle ABC a un
côté [BC] qui est diamètre de son cercle
circonscrit, alors ce triangle est rectangle en A et le
diamètre [BC] en est l'hypoténuse.
3. Soit un triangle ABC rectangle en A et H le
pied de la hauteur issue de A, alors AH2
= BH x HC. Réciproquement, soit ABC
un triangle et H le pied de la hauteur issue de A tel
que AH2 = BH x HC et que H
appartienne au segment [BC], alors ce triangle est rectangle en
A.
- Théorème
: propriétés du triangle équilatéral
1. Dans un triangle équilatéral, les trois angles sont
égaux en mesure (60°). Réciproquement, si dans un
triangle, les trois angles sont égaux en mesure (60°), alors
ce
triangle est équilatéral.
2. Dans un triangle équilatéral, les côtés
sont de même longueur. Réciproquement, si dans un
triangle, les trois côtés sont de même longueur,
alors ce
triangle est équilatéral.
3. Un triangle équilatéral possède trois axes de
symétrie orthogonale et un centre de rotation de 120° et de
240°. Réciproquement, si un triangle
possède deux axes de symétrie orthogonale, il est
équilatéral.
4. Dans un triangle équilatéral, les hauteurs,
médianes, médiatrices et bissectrices (issues d'un
même sommet) sont confondues.
Eléments pour une réciproque : - dans un triangle, une
médiatrice / médiane est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiatrice / hauteur est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiatrice / bissectrice est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiane / hauteur est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiane / bissectrice est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une hauteur / bissectrice est un axe
de symétrie orthogonale de ce triangle.
- Théorème
: propriétés du triangle isocèle
1. Dans un triangle isocèle, les deux angles à la base
sont égaux en mesure. Réciproquement, si dans un
triangle, deux angles sont égaux en mesure, alors ce
triangle est isocèle.
2. Dans un triangle isocèle, deux côtés sont de
même longueur. Réciproquement, si dans un triangle, deux
côtés sont de même longueur, alors ce
triangle est isocèle.
3. Un triangle isocèle possède un axe de symétrie
orthogonale. Réciproquement, si un triangle
possède un axe de symétrie orthogonale, il est
isocèle.
4. Dans un triangle isocèle, quatre droites particulières
(la hauteur issue du sommet principal, la médiane issue du
sommet principal, la médiatrice de la base principale et la
bissectrice issue du sommet principal) sont confondues. Eléments
pour une réciproque : - dans un triangle, une
médiatrice / médiane est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiatrice / hauteur est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiatrice / bissectrice est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiane / hauteur est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une médiane / bissectrice est un axe
de symétrie orthogonale de ce triangle ;
- dans un triangle, une hauteur / bissectrice est un axe
de symétrie orthogonale de ce triangle.
- Théorème
: l'inégalité triangulaire
Soient trois points A, B et C. On a AB + AC
≥ BC.
Lorsque AB + AC = BC, on a A qui appartient au segment [BC].
Résumés des précédents théorèmes sous une forme probablement plus facilement
mémorisable.

Exercice [Guadeloupe,
Guyane, 2000]
Quadrilatères
Un quadrilatère est un polygone à quatre
côtés.
Celui-ci peut être convexe ou non, et puis, être
croisé ou non.
- Exercice corrigé
Représenter de façon ensembliste les quadrilatères
usuels (carrés, rectangles, losanges, parallélogrammes,
trapèzes, trapèzes isocèles, trapèzes
rectangles, ..., quelconques). Ces patates classifient les
quadrilatères usuels.
Voici la représentation terminée...

Quelques quadrilatères particuliers ...
Le parallélogramme, le losange, le rectangle
et le carré
- Théorème
: caractérisations du parallélogramme
1.a) Un parallélogramme est un quadrilatère ayant ses
côtés opposés parallèles.
1.b) Réciproquement, un quadrilatère ayant ses
côtés opposés parallèles est un
parallélogramme (définition du parallélogramme).
2.a) Un quadrilatère convexe ayant ses côtés
opposés de même longueur est un parallélogramme.
2.b) Réciproquement, un parallélogramme est un
quadrilatère dont les côtés opposés sont de
même longueur.
3.a) Un quadrilatère convexe ayant deux côtés
opposés parallèles de même longueur est un
parallélogramme.
3.b) Réciproquement, un parallélogramme est un
quadrilatère ayant deux côtés opposés
parallèles de même longueur.
4.a) Un quadrilatère ayant ses diagonales qui se coupent en leur
milieu est un parallélogramme.
4.b) Réciproquement, un parallélogramme est un
quadrilatère dont les diagonales se coupent en leur milieu.
5.a) Un quadrilatère convexe ayant ses angles opposés
égaux en mesure est un parallélogramme.
5.b) Réciproquement, un parallélogramme est un
quadrilatère ayant ses angles opposés égaux en
mesure.
- Théorème
: caractérisations du losange
1.a) Un losange est un quadrilatère ayant quatre
côtés de même longueur.
1.b) Réciproquement, un quadrilatère convexe ayant quatre
côtés de même longueur est un losange (définition
du losange).
2.a) Un parallélogramme ayant deux côtés
consécutifs de même longueur est un losange.
2.b) Réciproquement, un losange est un parallélogramme
ayant deux côtés consécutifs de même
longueur.
3.a) Un parallélogramme ayant ses diagonales perpendiculaires
est un losange.
3.b) Réciproquement, un losange est un parallélogramme
dont les diagonales sont perpendiculaires.
Remarque : Tout losange est un parallélogramme. La
réciproque est fausse.
- Théorème
: caractérisations du rectangle
1.a) Un parallélogramme ayant ses diagonales de même
longueur est un rectangle.
1.b) Réciproquement, un rectangle est un parallélogramme
dont les diagonales sont de même longueur.
2.a) Un rectangle est un quadrilatère ayant quatre angles
droits.
2.b) Réciproquement, un quadrilatère ayant trois angles
droits est un rectangle (définition du rectangle).
3.a) Un parallélogramme ayant un angle droit est un rectangle.
3.b) Réciproquement, un rectangle est un parallélogramme
ayant un angle droit.
Remarque : Tout rectangle est un parallélogramme. La
réciproque est fausse.
- Théorème
: caractérisations du carré
1.a) Un rectangle qui possède deux côtés
consécutifs de même longueur est un carré.
1.b) Réciproquement, un carré est un rectangle qui
possède deux côtés consécutifs de même
longueur.
2.a) Un losange qui possède ses diagonales de même
longueur est un carré.
2.b) Réciproquement, un carré est un losange qui
possède ses diagonales de même longueur.
3.a) Un rectangle qui possède ses diagonales perpendiculaires
est un carré.
3.b) Réciproquement, un carré est un rectangle qui
possède ses diagonales perpendiculaires.
4.a) Un losange qui possède un angle droit est un carré.
4.b) Réciproquement, un carré est un losange qui
possède un angle droit.
5.a) Tout carré est à la fois rectangle et losange.
5.b) Réciproquement, un quadrilatère qui est à la
fois rectangle et losange est un carré (définition du
carré).
Remarque : Tout carré est un losange. La réciproque est
fausse.
Remarque : Tout carré est un rectangle. La réciproque est
fausse.
- Théorème
: caractérisations par les isométries du
parallélogramme, du losange, du rectangle et du carré
1.a) Un parallélogramme possède un centre de
symétrie.
1.b) Réciproquement, si un quadrilatère admet un centre
de symétrie, c'est un parallélogramme.
2.a) Un losange possède deux axes de symétrie
(orthogonale) perpendiculaires entre eux et un centre de
symétrie.
2.b) Un quadrilatère qui possède deux axes de
symétrie (orthogonale) distincts est un losange OU un
rectangle.
2.c) Un quadrilatère qui possède un axe de
symétrie (orthogonale) et un centre de symétrie est un
losange OU un rectangle.
3.a) Un rectangle possède deux axes de symétrie
(orthogonale) perpendiculaires entre eux et un centre de
symétrie.
3.b) Un quadrilatère qui possède deux axes de
symétrie (orthogonale) distincts est un losange OU un
rectangle.
3.c) Un quadrilatère qui possède un axe de
symétrie (orthogonale) et un centre de symétrie est un
losange OU un rectangle.
4.a) Un carré possède quatre axes de symétrie (les
diagonales et les médianes), un centre (l'intersection des axes
de symétrie) qui est centre de rotation de 90 degrés, de
180 degrés (i.e. un centre de symétrie) et de 270
degrés.
4.b) Réciproquement, un quadrilatère qui possède
trois axes de symétrie (orthogonale) est un carré.
Le trapèze
- Théorème
: caractérisations du trapèze
1.a) Un trapèze est un quadrilatère ayant deux
côtés opposés parallèles.
1.b) Réciproquement, si un quadrilatère a deux
côtés opposés parallèles, c'est un
trapèze (définition du trapèze).
2.a) Un trapèze rectangle est un trapèze qui
possède au moins un angle droit.
2.b) Réciproquement, un trapèze qui possède au
moins un angle droit, est un trapèze rectangle (définition
du trapèze rectangle).
3.a) Un trapèze rectangle est un quadrilatère qui
possède deux angles droits consécutifs.
3.b) Réciproquement, un quadrilatère qui possède
deux angles droits consécutifs est un trapèze rectangle.
4.a) Un trapèze isocèle est soit un rectangle, soit un
trapèze qui a trois de ses côtés,
considérés comme droites, qui forment un triangle
isocèle.
4.b) Réciproquement, un trapèze ayant trois de ses
côtés, considérés comme droites qui forment
un triangle isocèle, est un trapèze isocèle et un
rectangle est un trapèze isocèle (définition du
trapèze isocèle).
5.a) Un trapèze qui a deux côtés opposés
égaux est soit un trapèze isocèle, soit un
parallélogramme.
5.b) Réciproquement, un trapèze isocèle a deux
côtés opposés égaux.
6.a) Un trapèze qui a deux angles consécutifs
égaux est soit un trapèze isocèle, soit un trapèze rectangle.
6.b) Réciproquement, un trapèze isocèle a deux
angles consécutifs égaux.
7.a) Un trapèze isocèle est un trapèze qui
possède un axe de symétrie.
7.b) Réciproquement, un trapèze qui possède un axe
de symétrie est un trapèze isocèle.
7.c) Réciproquement, un quadrilatère qui possède
un axe
de symétrie est un trapèze isocèle OU un
losange.
Résumés des précédents théorèmes sous une forme probablement plus facilement
mémorisable.


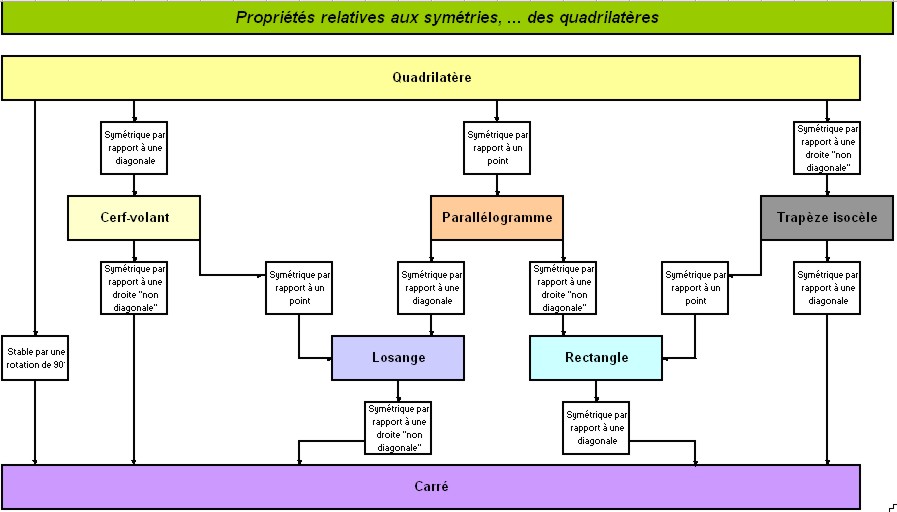
Exercice : trapèze
Exercice : milieu
Exercice : carré
Exercice : triangles isocèles
Exercice : alignement
Exercice [Créteil, Paris, Versailles, 2004]
Exercice [Aix,
Marseille, Corse, Montpellier, Nice, 1999]
Exercice [Créteil, Paris, Versailles, 1999]
Exercice [Montpellier,
1998]
Exercice : cocyclicité ...
Exercice [Orléans, Tours, 1998]
Exercice [Lyon, Grenoble, 1999]
Exercice [Aix-Marseille, 1998]
Exercice [Grenoble, 1998]
"Sujets zéros" pour la session
2006

Exercices diciplinaires corrigés de cette page.





